[Lightweight DL] Quantization (2/3)

지난 포스팅에 이어, 경량 딥러닝을 위한 기법 중 하나인 Quantization을 살펴보겠습니다.

 

Review.
딥러닝에서 quantization이란 모델의 weight과 activation을 나타내는 bit 수, 즉 bit depth를 줄이는 것을 의미합니다. 데이터 타입을 float32에서 float16, bfloat16으로 점차 줄여나가다가, Google과 Nvidia에서는 아예 int 연산으로 대체하자며 Int 8bit solution을 제시했습니다. 

 

본 글에서는 bit depth를 8보다 더 줄이기 위해, 즉 "sub" 8bit quantization으로 나아가기 위해 어떠한 연구들이 진행되었는지 살펴보도록 하겠습니다. 본 글은 서울대학교 유승주 교수님의 "Embedded Systems and Applications" 수업을 기반으로 정리했습니다. 

Intro. What is Quantization?
Int 8 Quantization - Google's solution
Int 8 Quantization - Nvidia's solution
Sub-8bit quantization - 1) Log Quantization
Sub-8bit quantization - 2) Weighted Quantization
Sub-8bit quantization - 3) Outlier Quantization
4bit quantization - 1) Precision Highway
4bit quantization - 2) Learnable Quantization
Sub-4bit quantization - PROFIT with MobileNet v3 case
Binary quantization

Sub-8bit quantization

Sub-8bit quantization - 1) Log Quantization

linear scale vs. logarithmic scale

Linear scale과 logarthmic scale의 차이를 직관적으로 보여주는 예시 사진입니다. Linear scale에서는 값의 크기에 상관 없이 값들의 간격이 1로 일정합니다. 반면 logarithmic scale에서는 값이 커짐에 따라 범위가 넓어진다는 것을 볼 수 있습니다. 이렇듯 값이 작은 범위에서는 간격이 촘촘하고, 값이 큰 범위에서는 간격이 널찍하다는 점이 logarithmic scale의 특성입니다.

Convolutional Neural Networks using Logarithmic Data Representation

Logarithm based quantization(LogQuant)은 linear scale이 아닌 logarithmic scale을 적용하여 값을 quantize하는 방식입니다. 위 그림은 VGG16모델 중 conv2_2 레이어의 activation 분포를 나타냅니다. 위에서부터 차례로 a) LogQuant 적용 전, b) LogQuant 적용 후, c) LinearQuant 적용 전, d) LinearQuant 적용 후의 그래프입니다. Linear quantization을 적용한 아래의 두 그래프에서는 x축(quantized value)의 간격이 일정한 데에 반해, log quantization을 적용한 위의 두 그래프에서는 간격이 촘촘하다가 점점 넓어지는 것을 볼 수 있습니다. 

 

이렇게 log scale로 quantize를 시킬 경우, 크게 두 가지 이점이 있습니다.

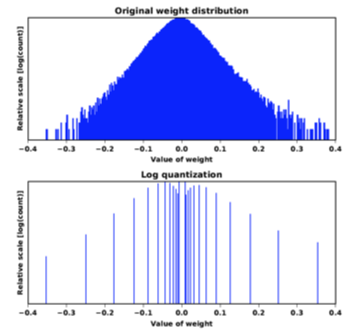
weight distribution (original vs. after log quantization)

첫째, quantization error가 감소합니다. 

위 그림에서 볼 수 있듯이, weight distribution 상에서 0에 가까운 작은 값들이 대부분을 차지합니다. 그 때문에 log quantization을 통해 작은 값들에서 촘촘한 간격으로 quantize해준다면, 전반적인 quantization error가 줄어들게 됩니다.

 

둘째, computation cost가 감소합니다.

Log quantization을 적용한다면, 원래의 값이 2의 거듭제곱으로 truncate됩니다. Convolution연산은 사실상 activation과 weight의 곱셈 연산으로 수행할 수 있는데요. 만약 activation에 log quantization을 시켰을 경우, 곱셈 연산을 bit shift연산으로 대체할 수 있게 됩니다. 곱셈 연산보다 shift연산이 더 빠르게 수행되기 때문에, 이는 computation cost의 감소로 이어집니다.

위 그림의 (a)는 activation과 weight 모두 float32 타입을 가지는 일반적인 경우에서의 convolution 연산을 나타냅니다. (b)는 LogQuant를 activation에만 적용시킨 경우, (c)는 LogQuant를 activation과 weight 양쪽에 적용시킨 경우의 convolution 연산을 나타냅니다.

 

이 중 (b) 그림에 대해 좀 더 자세히 설명하겠습니다. 앞서 설명했듯이, 곱셈 연산을 지수(exponent)만큼의 bit shifting 연산으로 대체할 수 있습니다. 그렇게 bit shift - accumulate 연산으로 convolution을 수행한 뒤, ReLU 활성함수에 통과시킵니다. 이렇게 계산된 activation값에 log quantization을 적용하면 2의 지수로 truncate됩니다. 보다 엄밀히 말하자면, 다음 convolution 레이어의 인풋으로도 지수(exponent)를 넘겨줘야 하기 때문에 그림에서와 같이 "leftmost 1의 position"을 계산하는 것입니다.

 

앞서 LogQuant의 장점을 언급했는데요, 당연히 단점도 있습니다. 0에 가까운 작은 값들에서는 촘촘한 간격으로 quantize하기 때문에 quantization error가 작아지지만, 그 반대로 큰 값들에 대해서는 quantization error가 커진다는 것이 단점입니다. 구체적인 숫자 예시를 들어 설명해보겠습니다.

위 그림은 (weight = 5.5, activation = 4.5)가 주어졌을 때, activation 값에 LogQuant를 적용하는 예시입니다.

1) (weight = 5.5)를 이진수로 나타내면 b101.1, (activation = 4.5)를 이진수로 나타내면 b100.1입니다.

2) Bit shift를 위해 (activation = b101.1)를 2의 지수로 truncate하면 b100.0가 됩니다. 

3) 이렇게 원래의 곱셈 연산(5.5 * 4.5)을 Bitshift(b101.1, 2)연산으로 대체하면 b10110(22)가 계산됩니다. 즉 5.5*4.5 = 24.75였던 원래의 값이 22로 줄어들었습니다.

4) 여기서 끝이 아니죠. (b)그림을 설명할 때 언급했듯이, 다음 레이어의 인풋으로 넘겨주기 위해 이 값도 2의 지수로 truncate해줘야 하기 때문에 b10000(16)이 됩니다. 

결과적으로 24.75가 16이 되어버리는, 상당한 quantization error가 발생한다는 사실을 확인해보았습니다.

위 표는 AlexNet과 VGG16 모델의 weight를 5bit로, activation을 4bit로 quantize한 결과를 나타냅니다. LogQuant로 인한 accuracy drop이 크지 않다는 것을 볼 수 있습니다. 

요약: Log quantization이란, linear scale이 아닌 logarithmic scale을 적용하여 값을 quantize하는 방식.
장점 - 더 많은 연산을 수행할 수 있으며 작은 값들에서 quantization error가 낮다
단점 - 큰 값들에서 quantization error가 크다
Log quantization의 장점이 존재함에도 불구하고 실제로는 linear quantization을 그냥 사용하는 추세라고 합니다. 아마 이미 bit depth가 많이 줄어들었기 때문에, post processing으로 인한 로드를 굳이 감당하느니 linear quantization을 사용하는 것이 아닌지 싶습니다. 최근 연구 동향에서는 linear quantization을 쓰면서 accuracy loss를 줄이는 것이 관건이라고 합니다.

Sub-8bit quantization - 2) Weighted Quantization 

위 그림에서 좌측 상단의 그래프는 original weight distribution을 나타냅니다. 우측 상단의 그래프는 지난 포스팅에서 소개한 Nvidia의 int8 솔루션, 즉 큰 값들을 truncate한 뒤 linear quantization을 적용한 분포를 나타냅니다. 좌측 하단의 그래프는 앞서 언급한 LogQuant를 적용한 분포를 나타냅니다. 마지막으로, 우측 하단의 그래프가 이제 설명할 Weighted entropy based quantization, 소위 weighted quantization을 적용한 분포입니다. 작은 값들에서 간격이 촘촘한 log quantization과 달리, weighted quantization 그래프에서는 중간 크기의 값들에서 간격이 촘촘하다는 관찰을 할 수 있습니다.

 

"Weighted entropy based quantization"은 무엇일지, 이름으로부터 힌트를 얻을 수 있는데요. 'Weighted entropy'라는 매트릭을 극대화시키는 방향으로 quantize를 적용하나보다, 정도로 추측한다면 훌륭한 직관입니다.

 

지난 포스팅에서 언급했듯이, Nvidia의 int8 솔루션에서는 KL divergence를 기준으로 information loss가 최소화되게끔 threshold를 설정했습니다. 하지만 이렇게 값들의 분포 차이만으로 information loss를 측정한다면, 값들의 크기(magnitude)는 고려되지 않게 됩니다. 그리하여 "large weights are important!"라며, 저자는 weighted entropy라는 메트릭을 제시합니다. 

 

위 수식에서 S가 weighted entropy입니다. 우변에서 I를 제외하고 PlogP만 있다면 우리가 흔히 아는 엔트로피 공식인데요. Weighted entropy는 일반적인 엔트로피 공식에 I라는 importance term을 첨가했습니다.

 

그렇다면 weighted quantization이 모델 학습 시에 어떻게 적용되는지 살펴보도록 하겠습니다. Weighted quantization은 쉽게 말해, weight들을 clustering하는 것입니다. 각 cluster마다 quantized value가 맵핑되어 있으면, weight들을 특정 cluster에 할당하는 것입니다. 위 그림은 cluster의 수가 N=4인 예시로, 빨간 선은 cluster들 간의 boundary 값을 나타냅니다. Cluster 수가 4개이기 때문에 cluster index는 2bit로 표현이 가능합니다. 이 때, boundary 값은 weighted entropy가 maximize되도록 결정됩니다. 

 

AlexNet과 GoogleNet에 대해 weighted quantizaion을 적용한 결과, full precision일 때에 비해 accuracy loss가 매우 작게 나타났습니다.

또한, 저자는 AlexNet에 대해 네 가지 configuration(DEC, INC, CONCAVE, CONVEX)으로 sensitivity analyisis를 수행함으로써 레이어 별로 quantization의 영향이 어떻게 달라지는지 관찰했습니다. Conv 레이어별로 bit depth를 달리 설정했을 때 accuracy가 어떻게 변하는지 관찰한 결과, 양 끝단의 레이어들이 quantization에 민감하다는 사실을 확인했습니다. 다시 말해 input과 output 근처의 레이어에서는 bit depth를 크게 설정하고, 중간에는 bit depth를 작게 설정한 경우에 가장 높은 accuracy가 측정되었습니다.

요약: Weighted quantization이란, weight들을 클러스터링하는 것.
클러스터의 boundary값은 weighted entropy를 극대화하는 방향으로 결정된다. 

Sub-8bit quantization - 3) Outlier Quantization

Outlier Quantization 역시 이름으로부터 추측이 가능한데요. 데이터 분포 상에서 outlier들(절대값이 큰 양 끝단의 값들)이 quantization error에 크게 기여한다는 관찰에서 비롯되었습니다. 그리하여 양 끝의 outlier들에는 quantization을 적용하지 않고, 그 사이에 있는 값들만 quantize하는 것이 바로 outlier quantization(OLQuant)입니다. 

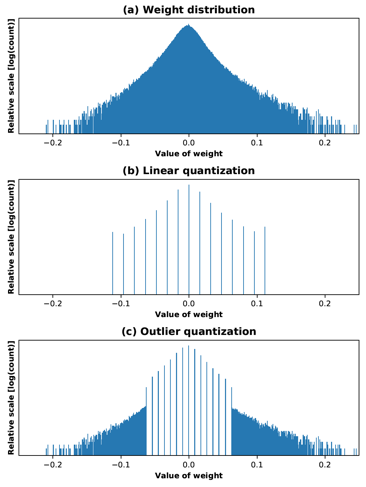
위 그림에서 알 수 있듯이, OLQuant를 적용할 경우 linear quantization을 적용하는 범위가 줄어들기 때문에 간격이 매우 촘촘해집니다. Outlier들(1~3%)에는 quantize하지 않기 때문에 quantization error가 아예 발생하지 않고, 사이에 있는 데이터들(97~99%)에는 촘촘한 간격으로 quantize하기 때문에 quantization error가 줄어들게 됩니다. 

 

AlexNet에서 outlier quantization을 적용한 경우, outlier ratio가 0.5%만 되어도 성능이 full precision에 준한다는 실험 결과가 나타났습니다.

OLQuant의 효과를 PCA visualization을 통해서도 직관적으로 알 수 있습니다. 위 그림의 (a)는 full precision모델에서 PCA를 적용한 것인데, 보다시피 값들이 잘 분리됩니다. 하지만 (b)는 linear quantization을 적용한 데이터로, 값들이 잘 분리되지 않았습니다. OLQuant를 적용한 것이 (c)와 (d)인데요. Outlier ratio를 0.1%로만 잡아도 (c)처럼 잘 분리되고, (d)에서와 같이 outlier ratio를 3%로 올렸더니 분리가 더 잘 된다는 것을 알 수 있습니다. 

 

참고로 quantization을 적용할 때 학습 과정에서 fine tuning을 통해 accuracy를 올리는 것이 일반적인데요. Fine tuning을 하면 결과가 좋아지는 것이 당연하지만, 대규모 데이터 센터에서 사용하는 규모가 큰 모델의 경우 fine tuning을 적용하기도 쉽지 않습니다. 하지만 OLQuant기법을 적용한다면 fine-tuning 과정을 거치지 않더라도 accuracy loss가 미미하다는 점이 장점입니다. 실제로 Facebook data center에서 outlier ratio 3%로 OLQuant를 적용한 결과, top-1 accuracy loss가 1% 미만이었으며 1.7x speedup(Intel CPU)을 낼 수 있었다고 합니다.

지금까지는 OLQuant를 적용하면 accuracy loss도 적고 inference time도 줄어든다는, test time에서의 이점을 설명했습니다.

그렇다면 test time이 아닌 training time에서 OLQuant를 적용하면 어떤 이점이 있을지 생각해볼 차례입니다.

 

딥러닝 모델은 학습 과정에서 메모리 사용량이 엄청난데요. Back propagation을 수행하기 위해 intermediate activation들을 다 저장해줘야 하기 때문입니다. 이 때, 일반적으로 weight의 크기보다 activation의 크기가 훨씬 크기 때문에, activation 값들의 bit depth를 줄이면 메모리 상의 이점이 분명히 있을 것입니다.

ResNet-50모델에서 ReLU 레이어들에 대해 outlier ratio 2%로 3bit OLQuant를 적용한 결과, activation값들이 차지하는 메모리 공간이 9배 줄어들고 training accuracy는 거의 유지되었다고 합니다. 어떻게 training accuracy가 유지될 수 있었는지 의문이 들 수 있는데요, "ReLU"레이어들에 대해서만 OLQuant를 적용했다는 것이 힌트입니다. 

 

Training accuracy가 유지되었다는 것은, backward pass시 weight update를 할 때 quantization의 영향이 크지 않았다는 것을 의미하는데요. OLQuant를 학습 과정에서 어떻게 적용하는지 공식과 함께 살펴보며 그 이유를 알아보도록 하겠습니다.

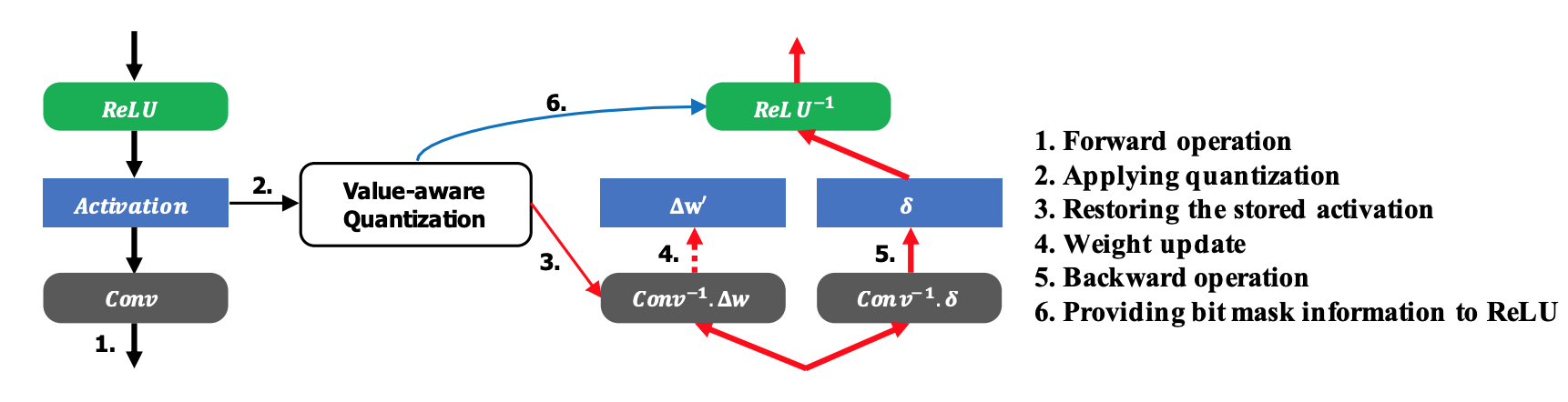
위 그림은 OLQuant의 학습 과정을 나타냅니다. 저자는 "quantized back-propagation"라 하여, forward pass는 full precision으로 수행하되 backward pass에 사용되는 activation값에만 OLQuant를 적용하는 기법을 제시합니다. 

 

 

위 그림에서 왼쪽 식은 weight update가 계산되는 공식을 나타냅니다. 첫번째 항인 learning rate는 상수이기 때문에 배제하고, 나머지 두 항들에 주목하겠습니다. 

 

두번째 항인 propagated delta(local gradient)는 오른쪽 식으로 풀어쓸 수 있습니다. 이 때, Relu함수의 경우 derivative가 0또는 1로, activation에 quantize를 적용하든 말든 derivative가 일정합니다. 즉 weight를 update하는 상황에서 relu activation을 quantize하더라도, propagated delta와 learning rate에는 변화가 없다고 말할 수 있습니다.

 

Bit depth를 3 또는 4로 설정하는 소위 'aggressive quantization'을 적용하더라도, 이렇게 weight update 과정에서만 precision loss가 발생하기 때문에 training accuracy가 크게 떨어지지 않았다고 합니다. ResNet-50모델의 학습에 outlier ratio 2%로 3bit quantization을 적용한 결과, accuracy는 유지되고 activation이 차지하는 메모리는 6.1배로 감소했습니다. 

요약: Outlier quantization이란, outlier들은 quantize하지 않고 그 사이의 값들에만 linear quantization을 적용하는 기법.
Test time에서 weight에 outlier quantization을 적용할 경우, 낮은 accuracy loss로 inference time을 크게 감소시킬 수 있다.
Training time에서 activation에 outlier quantization을 적용할 경우, 낮은 accuracy loss로 메모리 사용량을 크게 감소시킬 수 있다. 

4bit quantization

4bit quantization - 1) Precision Highway

Quantization error가 레이어마다 누적되어 끝으로 갈수록 눈덩이처럼 불어난다는 문제를 저자는 "accumulated quantization error problem"이라 일컫는데요, 이를 해결하기 위해 precision highway라는 기법을 제안합니다. 

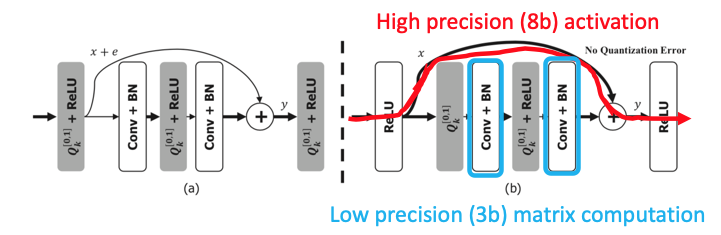
위 그림은 ResNet에서 residual block을 나타냅니다. ResNet에 precision highway를 적용한다는 것은, skip connection에는 bit depth를 크게 설정하고, 레이어들을 통과하는 부분에서는 bit depth를 작게 설정하는 것을 의미합니다.

 

ResNet의 identity shortcut 작동 방식을 기억해봅시다.

Residual block의 출력이 F(x)+x인데, F(x)는 0이 되는 방향으로 학습되기 때문에 크기가 작습니다. 즉 상대적으로 크기가 큰 x를 high precision으로 잡고 연산을 수행할 경우, 전반적인 quantization error가 감소할 것입니다.

 

또한, F(x)+x을 계산하는 덧셈 연산만 큰 bit depth로 수행하고, 연산의 대부분을 차지하는 matrix multiplication는 작은 bitwidth로 수행하기 때문에 연산량 차원에서도 이득이라 할 수 있습니다. 실제로 (3-bit matrix computation + 8-bit skip connections)의 조합으로 실험을 수행한 결과 full precision모델의 accuracy에 준했다고 합니다.

4bit quantization - 2) Learnable Quantization 

Learnable quantization이란, truncation threshold나 pruning threshold와 같은 값들을 trainable 파라미터로 설정하여 학습시키는 것을 의미합니다. 

Learnable quantization에는 대표적으로 두 가지 기법, PACT와 QIL이 있습니다. 이들 모두 ReLU activation function을 타겟하였고, 위 그래프에서 p, c, d와 같은 파라미터들을 학습을 통해 알아내자는 differentiable quantization을 제시합니다.

Sub-4bit quantization - PROFIT with MobileNet v3 case

지금까지 설명한 기법들의 경우, ResNet과 같이 거대한 모델들에 quantization을 적용한 실험들을 수행했습니다. 하지만 실제 use case를 생각해본다면, 리소스가 적은 디바이스에서 돌리려면 애초에 거대한 모델이 아닌 optimized 모델들을 사용하지 않을까요? 즉 ResNet과 같은 모델이 아닌, MobileNet 또는 SqueezeNet과 같이 이미 optimized된 모델들을 활용할 경우가 더 많을 것입니다. 이미 optimize된 모델에 quantization을 적용해도 연산량은 줄이고 성능은 유지되게끔 하는 것이 보다 실질적인 challenge라고 볼 수 있습니다. 

그래서 MobileNetv3에 4bit quantization을 적용하려고 봤더니, 다음 두 가지 문제가 있었다고 합니다.

문제 1. h-swish 함수로 인한 quantization 에러

문제 2. weight quantization으로 인한 activation instability

각 문제가 무엇이며, PROFIT에서는 이를 어떻게 해결했는지 설명하겠습니다. 

 

문제 1. h-swish 함수로 인한 quantization 에러

위 그림의 좌측 그래프에서 파란 선으로 표시된 것이 ReLU 활성함수, 노란 선으로 표시된 것이 H-swish 활성함수입니다. MobileNetv3에서는 h-swish라는 새로운 활성함수를 사용해서 성능을 개선했는데요. 0에 가까운 작은 숫자들에서 ReLU와 h-swish 함수의 출력값들이 다르다는 것을 볼 수 있습니다.

 

즉, ReLU를 사용하면 함수의 결과값이 0 또는 양수이지만, h-swish를 사용하면 함수의 결과값으로 "near-zero negative value"들이 존재하게 됩니다.이러한 음수 값들을 quantize해주기 위해 unsigned가 아닌 signed value로 quantize를 해주어야 하는데요. 위 그림의 우측 그래프에서 볼 수 있듯이, 음수 영역에서 버려지는 quantization level이 발생하는 것을 알 수 있습니다. 

이를 해결하기 위해 저자는 위와 같은 해결책을 제시합니다. Convolution 연산은 기본적으로 선형 함수, f(a+b)=f(a)+f(b) 성질을 만족하는 함수입니다. 즉 Conv(X)는 Conv(X+d) + Conv(-d)로 계산할 수 있습니다. activation 결과값인 X를 -d만큼 shift해서, X+d가 0또는 양수가 되게 한다면, 이를 unsigned 값으로 quantize시킬 수 있습니다. 그렇다면 앞서 언급했던 버려지는 음수 영역이 발생하지 않겠지요. 그리고 이 때 d는 상수이기 대문에, Conv(-d)는 training time에서 미리 계산할 수 있고, 이를 batch normalization의 bias로 설정해준다면 계산량이 더 늘지도 않아서 연산량 차원에서도 이득입니다.

문제 2. weight quantization으로 인한 activation instability

위 그림에서 좌측 두 개의 그래프를 봅시다. 빨간 선으로 표시된 그래프는 간격이 좀 더 좁은 high precision quantization을 적용한 경우이고, 파란 선으로 표시된 그래프는 간격이 좀 더 넓은 low precision quantization을 적용한 경우인데요. delta라는 아주 작은 값만큼 weight를 update시켰을 때, low precision quantization의 경우 x축의 간격이 더 넓은만큼 activation값도 더 큰 폭으로 변한다는 것을 볼 수 있습니다. 

 

이러한 activation instability가 문제인 이유는 batch normalization과 관련이 있습니다. 기억이 잘 나지 않는 분들을 위해 batch normalization에 대해 간단히 설명하자면 다음과 같습니다. 네트워크의 레이어에서 input의 distribution이 달라지는 현상을 internal covariance shift라고 하고, 이는 activation instability의 주된 원인으로 나타났습니다. 이러한 현상을 막기 위해 training시에 mini-batch 내의 mean과 variance를 구하고, 그를 사용하여 normalize시켜줍니다. 그리고 학습 과정에서 계산된 모든 batch mean과 variance의 moving average를 계산하여 test time에 활용하는 것이 batch normalization의 기본 아이디어입니다. 

 

즉 quantization으로 인해 activation의 분포가 원래의 분포와 많이 달라질 경우, 계산된 moving average도 사실상 원래의 분포를 반영하지 못하기 때문에 internal covariance shift현상을 막지 못하는 것입니다. 

이러한 "Activation Instability due to Weight Quantization"(AIWQ)를 수치화하기 위해, 저자는 "AIWQ distance"라는 메트릭을 제시합니다. 위 공식에서의 Dl로, 피쳐맵에 대해 weight update 이전의 activation 분포와 이후의 activation 분포의 channel-wise KLdivergence를 계산하고, 레이어 별로 이를 평균 취한 값입니다. 

위 그림은 MobileNetv3에서 사용된 세 가지 convolution 레이어 - depthwise layer, reduction(pointwise) layer, expansion layer - 에 대해 AIWQ distance를 나타낸 그래프입니다. x축은 레이어 인덱스로, 우측으로 갈수록 output layer에 가까워집니다. 보다시피 유독 depthwise layer에서, 특히 output layer에 가까워질수록 AIWQ distance가 크게 나타난다는 사실을 관찰할 수 있습니다. 그렇다면 depthwise layer는 왜 이렇게 weight quantization의 영향을 많이 받을까요?

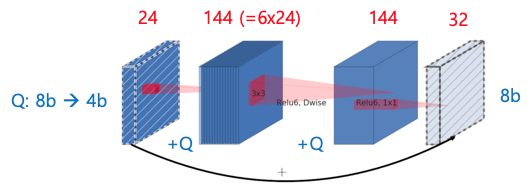
Depthwise layer의 경우 애초에 weight 수가 적기 때문에, averaging 효과가 적기 때문입니다. 위 그림은 MobileNetv3의 inverted residual block의 한 샘플입니다. 필터 사이즈가 3x3이기 때문에 depthwise layer의 weight 수가 9개인 반면, pointwise layer는 weight 수가 144개입니다. MobileNetv3의 inverted residual block 특성상 필터 갯수를 확 늘려주기 때문에, pointwise layer는 weight 수가 상대적으로 많아서 그로 인한 averaging 효과를 누리게 됩니다. 하지만 depthwise layer는 그렇지 못하기 때문에 weight quantization의 영향을 많이 받게 되는 것이지요. 

다시 아까의 그림이 등장했는데요. Output layer에 가까워질수록 AIWQ distance가 크게 나타난다는 점에서 착안하여, 저자는 training이 끝나갈 때 conv weight들을 "incremental freezing"하는 방법을 제시합니다.

1) AIWQ distance가 큰 conv layer들의 1/3을 freeze하고, 나머지 2/3의 conv layer와 bn layer를 학습합니다. 

2) 같은 방식으로 추가적으로 1/3의 conv layer를 freeze하고, 나머지 1/3의 conv layer와 bn layer를 학습합니다.

3) 남은 1/3까지 모든 conv layer를 freeze하고, bn layer만 학습합니다. 

이렇게 "incremental freezing"을 통해 얻은 batch mean과 variance를 test time에 활용한 결과 running mean, variance의 fluctuation이 감소하는 효과를 볼 수 있었다고 합니다. 

일반적으로 첫번째 레이어와 마지막 레이어는 quantization의 영향을 많이 받기 때문에, 이를 아예 배제하는 quantization 기법들도 많다고 합니다. 하지만 PROFIT에서는 첫번째 레이어와 마지막 레이어를 포함한 모든 레이어에 linear quantization을 적용했음에도 불구하고 좋은 성능을 낸다는 점에서 의의가 있습니다. ImageNet 데이터셋으로 MobileNetv1, MobileNetv2, MobileNetv3, MNasNet-A1모델에 대해 실험한 결과, 위 표에서 볼 수 있듯이 full precision accuracy에 준하는 결과가 나타났습니다. 

 

Summary

본 포스팅에서는 bit depth가 8보다 작은 quantization 기법들을 알아보았습니다. 다소 내용이 많지만, 관찰된 문제점에 대해 해결책을 제시하는 공통적인 흐름에 주목한다면, 그리 어렵지 않게 느껴질 것입니다. 다음 포스팅에서는 가장 극단적인 quantization인 binarization을 소개하고, 이를 구현한 과정을 코드와 함께 정리해보겠습니다.