[Lightweight DL] Quantization (1/3)

딥러닝 모델을 서버에서 학습하고 추론할 경우, Nvidia GPU와 같은 강력한 컴퓨팅 리소스들을 활용할 수 있습니다. 하지만 모바일/임베디드 환경에서는 컴퓨팅 리소스가 현저히 부족하기 때문에, 디바이스에서 학습은 커녕 추론을 하기까지도 많은 챌린지가 존재합니다. 기존 딥러닝 모델의 정확도를 크게 떨어뜨리지는 않으면서도, 적은 컴퓨팅 리소스로도 실행 가능할 수 있도록 경량 딥러닝(Lightweight Deep Learning) 분야의 연구가 활발히 진행되고 있습니다. 이를 위해 여러 가지 기법들이 존재하지만, 우선 본 포스팅에서는 Quantization(양자화)에 대해 살펴보고자 합니다. 본 글은 서울대학교 유승주 교수님의 "Embedded Systems and Applications" 수업을 기반으로 정리했습니다.

 

목차는 다음과 같습니다. 

Intro. What is Quantization?
Int 8 Quantization - Google's solution
Int 8 Quantization - Nvidia's solution
Sub-8bit quantization - 1) Log Quantization
Sub-8bit quantization - 2) Weighted Quantization
Sub-8bit quantization - 3) Outlier Quantization
4bit quantization - 1) Precision Highway
4bit quantization - 2) Learnable Quantization
Sub-4bit quantization - PROFIT with MobileNet v3 case
Binary quantization

Quantization시리즈는 총 세 개의 포스팅으로 나누어 정리할 예정입니다. 그 중 첫번째인 본 글에서는 quantization에 대한 기본 배경 지식 및 Int 8bit quantization을 다루었습니다. 다음 글에서는 비트 수를 8에서 4로, 4에서 2로 더 줄여나가기 위해 진행되어온 연구들을 소개하겠습니다. 그리고 마지막 글에서는 가장 극단적인 quantization이라 할 수 있는 binary quantization에 대해 소개하고, 이를 구현한 과정을 코드와 함께 정리할 예정입니다. 

Intro. What is Quantization?

Quantization이라는 용어가 비단 딥러닝에 국한된 것은 아닙니다. 위키피디아에 의하면, quantization의 정의는 다음과 같습니다. "Process of constraining an input from a continuous or otherwise large set of values (such as the real numbers) to a discrete set (such as the integers)".

 

촘촘한 값들을 듬성듬성하게 맵핑했다, 라고 대충 이해할 수 있는데요. 아직 잘 안 와닿을 수 있으니, 일상 속 quantization의 예시를 몇 가지 들어보겠습니다.

 

time.navyism.com 표준시간

누군가 현재 시간을 물어봤다고 가정합시다. "현재 시각은 2020년 11월 29일 18시 16분 16초 460밀리초야", 라고 답변해줄 수도 있겠습니다. 하지만 "18시 16분"이라고 답변해도 괜찮을 것이며, 더 나아가서는 "6시 반"이라고만 해줘도 충분할 것입니다. 정확한 현재 시각까지 알아야 할 필요가 없을때 적당히 precision이 낮은 값을 제공하는 것, 우리는 이미 quantization을 일상 속에서 실천하고 있네요 :D

출처: azooptics.com

또 다른 예시입니다. 이미지의 각 픽셀을 몇 bit로 표현할지를 bit depth라고 하는데요. 위 사진에서  볼 수 있다시피, bit depth가 늘어날수록 그라데이션이 세밀해집니다. 하지만 화면 크기가 작은 휴대폰으로 보기에는 bit depth 8짜리나 16짜리나 크게 다르지 않기 때문에, 8bit로 표현된 이미지를 유저에게 제공해도 충분할 것입니다. 

 

일반적인 문맥에서 quantization이란 무엇인지 두 예시를 통해 살펴보았습니다. 그렇다면 딥러닝 context에서의 quantization이 무엇인지 충분히 유추할 수 있을 텐데요. 바로 딥러닝 모델의 weight과 activation를 나타내는 bit 수를 줄이는 것입니다.

 

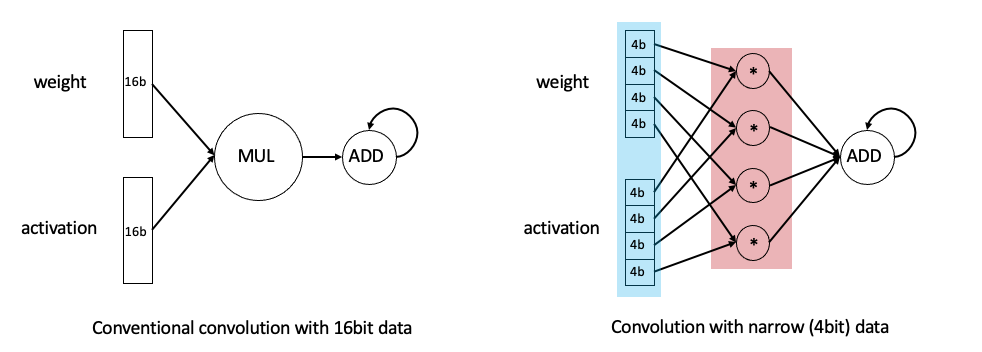
이렇게 bit 수를 줄일 경우 크게 두 가지 이점이 있습니다.
첫째, 데이터를 표현하는 bit 수가 줄어들기 때문에 모델이 차지하는 메모리 공간이 작어집니다.
둘째, 실행할 수 있는 연산의 수가 많아집니다.

두번째 이점에 대해 부연 설명을 하기 위해 위 그림을 삽입했습니다. 좌측(Conventional convolution with 16bit data)에서는 16bit짜리 데이터의 곱셈과 덧셈을 수행하고 있는 반면, 우측(Convolution with narrow 4bit data)에서는 4bit짜리 곱셈 네 번을 병렬적으로 수행한 뒤 덧셈을 수행하고 있습니다. 인풋 데이터를 표현하는 bit 수가 줄어들기 때문에, 동일한 하드웨어로 같은 시간 동안 수행할 수 있는 연산의 수가 더 많아지는 것입니다. 

Int-8bit quantization에 대해 본격적으로 들어가기에 앞서, 워밍업으로 bfloat16를 언급하고 넘어가겠습니다. 컴퓨터 아키텍쳐를 공부하신 분들, 혹시 부동소수점(floating point) representation관련 챕터 기억나시나요? "Exponent bit는 range를 결정하고, Mantissa bit는 precision을 결정한다", 이 정도 기억나면 충분합니다.

위 그림에서 볼 수 있듯이, 기존의 부동소수점 포맷인 float32는 (exponent 8bit) + (mantissa 23bit)로 구성되고, float16는 (exponent 5bit)과 (mantissa 10bit)로 구성됩니다. 

그러던 중, Google Brain에서는 bfloat16(Brain Floating Point Format)라는 새로운 포맷을 제시합니다. bfloat16는 (exponent 8bit)를 사용함으로써 float32만큼 넓은 range를 표현하되, (mantissa 7bit)를 사용함으로써 precision을 희생하는 부동소수점 포맷입니다. bfloat16 포맷은 구글에 의해 개발된 이후, 구글과 인텔에서 채택되어 실제 hardware accelerator에 적용되어 왔습니다.

 

여기서 더 나아가, 8bit만으로도 충분하다면서 구글과 Nvidia에서 솔루션을 각각 제시하는데요. 각각에 대해 설명해보겠습니다.

요약: Quantization이란 input distribution을 output distribution으로 맵핑하는 것. 이 때 발생하는 quantization error을 최소화시키고 기존 모델의 precision과 근사한 성능을 내려면 어떻게 해야하는지가 연구자들의 관심사.

Int 8 Quantization - Google's solution

Google에서 제시한 Int 8bit solution은 위 그림 한 장으로 요약할 수 있습니다. 상단의 노란색 격자(x) 표시들이 기존의 float 데이터를 의미하고, 하단의 노란색 격자(x)표시들이 quantize된 integer 데이터를 나타냅니다. 이를 수식적으로 이해해보도록 하겠습니다. 우선 간단한 예제를 통해 32-bit float를 8-bit integer로 변환시키는 방법을 살펴본 뒤, 이를 통해 float로 구성된 행렬의 곱셈 연산을 integer 연산으로 치환할 수 있음을 확인해보겠습니다. 

a. 32-bit float => 8-bit unsigned integer 

r : 기존의 float 데이터 (32-bit)
q : quantize된 integer 데이터 (8-bit unsigned)
S: scale factor
Z: 기존 데이터 분포 상에서 "0"이 quantized 데이터 분포 상에서 맵핑되는 값

기초 통계에서 표준화 시키는 공식이랑 느낌이 비슷하죠? 기존의 float 데이터 r이 주어졌을 때, 이를 S만큼 scale해주고 원점을 Z만큼 이동해주면 정수 데이터 q를 얻게 됩니다. 즉, S와 Z가 주어진다면 기존 분포의 데이터를 모두 quantize시킬 수 있겠죠. 기존 데이터의 분포가 다 다르기 때문에, 특정 데이터 분포가 주어졌을 때 S와 Z를 계산해줘야 하는데요. 간단한 예제를 통해 S와 Z를 계산해보도록 하겠습니다.

우선, q = ceil(r / S) + Z 라는 공식은 r = S (q - Z) 로 변환될 수 있습니다. 기존 분포에서 최솟값이 -31.4, 최댓값 65.7일 때 위 식에 대입하면 우측의 두 방정식이 구해집니다. 그리고 이를 연립하면 아래와 같은 계산을 통해 S=0.38, Z=83이 구해집니다.

즉, 기존 분포의 최솟값과 최댓값이 주어졌을 경우 S와 Z를 구할 수 있습니다. 그리고 S와 Z가 구해지면, q = ceil(r / S) + Z 공식에 대입함으로써 quantize된 데이터 q를 계산할 수 있습니다. r = 10.5를 대입하면 위 그림에서와 같이 q = 112가 계산됨을 쉽게 확인할 수 있습니다. 

b. Matrix multiplication (float --> integer)

Google에서는 이러한 INT8 solution을 통해 floating point 연산을 integer-only 연산으로 대체하고자 했습니다. 위에서 설명한 공식 r = S (q - Z) 을 적용하면, 각 원소가 floating point인 행렬의 곱셈을 아래와 같이 변환할 수 있습니다.

즉 아래의 공식으로 정리되는데, 이 식에서 M을 제외한 모든 값들이 정수입니다. 각 원소가 floating point인 행렬의 곱셈이 integer 연산으로 치환됨을 확인했습니다. 

이 때, 만약 Z1과 Z2가 0이 된다면 어떨까요? 아래 그림과 같이 식이 더욱 간결해질 것입니다. 

이러한 발상에서 기인하여 Z를 0으로 설정한 "zero matching case"를 설명해보겠습니다. 

c. 32-bit float => 8-bit signed integer (Zero Matching Case)

 

하지만 모든 것에는 tradeoff가 있는 법! 이러한 Zero matching case에서는 computation이 줄어드는 만큼 accuracy도 함께 줄어드는 경향이 관찰되었는데요. 아래 그림을 통해 살펴보겠습니다.

(위) general quantization (아래) zero matching case (Z=0)

Z가 83에서 0이 되면서 두 가지 변화가 생겼습니다. 첫째, scale factor인 S가 0.38에서 0.52로 커졌고, 둘째, quantized 데이터의 분포 상에서 -127에서 -60까지의 범위는 사실상 안 활용되고 있음을 관찰할 수 있습니다. 이러한 요인들로 인해 zero matching case에서는 precision이 더 낮아지는 결과가 나타났습니다. 즉, Z=0으로 설정할 경우 matrix computation이 가벼워지는 계산 상의 이점이 있으나, precision이 낮아진다는 tradeoff가 존재합니다.

 

Google의 INT8 solution을 요약하자면, 기존 분포에서 절댓값이 가장 큰 값을 127(또는 -127)로 맵핑하는 것입니다. 이러한 단순한 방식에서는 quantization error가 클 수 밖에 없는데요. 예를 들어 (-900, 900)범위의 분포와 (-200, 200)범위의 분포를 모두 (-100, 100)범위의 분포로 맵핑할 경우, 전자에서의 precision loss가 더 클 수밖에 없을 것입니다. 왜냐하면 (-900,900)범위의 분포에서는 892~900까지의 값이 모두 100으로 맵핑되고, (-200, 200)범위의 분포에서는 199와 200만 100으로 맵핑되기 때문입니다. 

 

이렇듯 quantization error는 맵핑되는 기존 분포의 데이터 범위 크기에 비례합니다. 이러한 점을 고려하여 precision을 개선하고자 한 Nvidia의 INT8 solution을 보도록 하겠습니다. 

Int 8 Quantization - Nvidia's solution

NVIDA에서 제시하는 Int 8bit solution에서는, truncation을 통해 기존 분포의 데이터 범위를 좁혀버립니다. 특정 threshold T를 넘어서는 값들을 모두 T로 truncate시켜준 뒤, -|T|~|T| 범위의 데이터를 -127~127 범위로 맵핑하는 것입니다. 이렇게 되면 기존 분포의 데이터 범위가 줄어들기 때문에, quantization error가 감소하게 됩니다. 하지만, 양 극단의 값들에서는 truncation error가 발생하겠죠. 이를테면 threshold가 "200"일 경우, "984"도 "201"도 모두 "200"으로 truncate되기 때문입니다. 즉 이러한 truncation error를 고려해야 하기 때문에, threshold값 T를 어떻게 정할지가 중요해집니다.

Threshold값 T를 어떤 값으로 설정하는 게 좋을까요? 쉽게 생각해서, information loss가 가장 작아지게끔 threshold 값을 설정해야겠죠.  Threshold 값의 모든 후보들에 대해 KL divergence(기존 분포: P, quantize된 분포: Q)를 계산한 뒤 loss가 최소화되는 값으로 T를 설정하는 것이 Nvidia에서 제시한 solution입니다. 

위 표에서 볼 수 있듯이, 이러한 Nvidia Int 8 solution을 적용시켜도 accuracy loss가 크지 않다는 사실을 확인할 수 있습니다.

Summary

본 포스팅을 통해 quantization이란 무엇인지, 그리고 Google과 Nvidia에서 제시한 commercial Int 8 solution들이 무엇인지 알아보았습니다. 비트 수를 줄임으로써 computation cost를 줄이되, precision은 기존 모델에 준하도록 유지하는 것이 딥러닝에서 quantization의 목적입니다. 다음 포스팅에서는 비트 수를 8보다 더 줄이기 위해 어떠한 연구들이 진행되었는지 살펴보도록 하겠습니다.