[Lightweight DL] Quantization (3/3)

Quantization 시리즈의 마지막 포스팅입니다. 

첫번째 포스팅에서 quantization이란 무엇인지 설명하고, int 8bit 솔루션들을 소개했습니다.

두번째 포스팅에서는 더 나아가 sub 8bit, sub 4bit quantization을 위해 진행된 연구들을 살펴보았습니다.

본 글에서는 binary quantization, 즉 binarization에 대해 소개하겠습니다. 

Review.
Sub-8bit quantization에서 총 세 가지 기법 - log quantization, weighted quantization, outlier quantization을 소개했습니다.
4bit quantization에서는 precision highway와 learnable quantization을 소개했습니다.
Sub 4bit quantization에서는 PROFIT with MobileNet v3 case 라는 연구를 소개했습니다. 
마지막 연구의 경우, 이미 optimize된 모델인 MobileNet v3에 quantization을 적용해도 효과가 있음을 보여줬다는 점에서 의의가 있었습니다.

본 글은 서울대학교 유승주 교수님의 "Embedded Systems and Applications" 수업을 기반으로 정리했습니다. 

Intro. What is Quantization?
Int 8 Quantization - Google's solution
Int 8 Quantization - Nvidia's solution
Sub-8bit quantization - 1) Log Quantization
Sub-8bit quantization - 2) Weighted Quantization
Sub-8bit quantization - 3) Outlier Quantization
4bit quantization - 1) Precision Highway
4bit quantization - 2) Learnable Quantization
Sub-4bit quantization - PROFIT with MobileNet v3 case
Binary quantization - 1) Binary-Weight-Network
Binary quantization - 2) XNOR Network
Binary quantization - 3) ReActNet

Binary quantization

Nvidia에서 약 세 달 전에 공개한 A100 Tensor 코어 GPU는 int-8bit, int-4bit은 물론, binary computation도 가능합니다. 

위 그림은 input operand의 데이터 타입에 따른 V100, A100 GPU의 성능을 보여주고 있습니다. 모델을 binarize한다면 A100 GPU에서 4992TOPS라는 엄청난 성능을 취할 수 있겠네요. 그렇다면 binary quantization이 무엇이며 어떤 모델들이 제시되어 왔는지 본격적으로 살펴보겠습니다.

FLOPS, TFLOPS, TOPS는 컴퓨터의 성능 지표(Performance metric)입니다.

FLOPS(Floating point Operations Per Second)는 말 그대로, 초당 부동소수점 연산 횟수를 나타내는 수치입니다. 즉 컴퓨터가 1초동안 수행할 수 있는 부동소수점 연산의 횟수를 의미합니다.

 

TFLOPS(Tera Floating point Operations Per Second)에서 "Tera"는 1조를 나타냅니다. 즉 1TFLOPS는 1초에 1조 번의 부동소수점 연산을 하는 것입니다. 슈퍼컴퓨터의 계산 속도를 나타내는 성능 지표로 TFLOPS가 주로 쓰입니다. 

 

TOPS(Tensor Operations Per Second)는 초당 텐서 연산 횟수를 나타내는 수치입니다. 딥러닝 프로세서의 계산 속도를 나타내는 성능 지표로 TOPS가 주로 쓰입니다. 

 

Quantization은 딥러닝 모델의 weight과 activation을 나타내는 bit 수를 줄이는 것입니다. 그렇다면 Binary quantization은 bit depth가 1인가보다, 라고 쉽게 추측할 수 있습니다.

 

Weight과 activation 중 어느 것을 binary representation으로 나타낼지, 혹은 둘 다 binary representation으로 나타낼지 여러 경우가 존재할텐데요. 초기에 제시된 모델인 binary weight network는 weight만 binary로 나타내고, activation은 float32로 나타냅니다. 이후 제시된 모델 XNOR network는 weight과 activation을 모두 binary로 나타냅니다.

 

Binary weight network와 XNOR network는 둘 다 2016년에 제시된, 상당히 오래된 모델들인데요. 올해(2020) 제시된 따끈따끈한 모델, ReActNet도 소개하도록 하겠습니다.

Binarization - 1) Binary Weight Network

Binary weight network에서는 weight 값들을 binarize합니다. 이 때, binarize한다는 것은 기존의 값을 1 또는 -1로 맵핑하는 것을 의미합니다. 예를 들어, 기존의 weight가 0.12면 1로 맵핑하고, 기존의 weight가 -1.4면 -1로 맵핑하는 것이 가장 단순한 방법이겠지요.

 

이렇게 부호만으로 맵핑하는 단순한 방식은, 간단한만큼 허점이 있을텐데요. 기존 값의 magnitude가 고려되지 않는다는 점입니다. 이를테면 1.4와 0.2 둘 다 양수이기 때문에 1로 맵핑되는데, 이렇게 크기가 7배나 차이나는 두 값들이 같은 값으로 맵핑된다면 quantization error가 매우 커질 것입니다. 

기존 weight들의 magnitude를 고려한 binary quantization을 수행하기 위해, 위 그림에서의 알파와 같이 global scaling factor를 둡니다. 물론 이렇게 해도 모든 element에 대해 element-wise로 magnitude를 고려해주지는 못합니다. 하지만 적어도 (0.12, 0.1, -0.0.08)는 알파가 0.1로, (1.2, -2.0, -1.6)는 알파가 1.6으로 계산되는 식으로, 스케일을 고려한 quantization이 수행될 것입니다. 

 

그렇다면 B와 alpha는 어떻게 계산될까요? 문제는 다음과 같이 정의할 수 있습니다. 

사실 직관적으로 충분히 해를 구할 수 있는 문제이기 때문에, 먼저 한 번 추측해봅시다. B는, 맨 처음에 예시로 들었듯이, 부호에 따라 양수는 1로 맵핑하고 음수는 -1로 맵핑해서 구할 수 있을 것입니다. 그렇게 된다면 alpha는 어떻게 될까요? weight들의 평균으로 하면 될 것 같습니다. 

 BTB, WTW가 상수이기 때문에 원래의 문제인 argmin(J)가 argmax(WTB)로 치환됩니다

argmax(WTB)의 해 B는 자명하게 구해집니다. 그를 대입하면 alpha도 위와 같이 계산됩니다.

바로 그 추측이 맞다는 것을 위 증명을 통해 확인할 수 있습니다. 매우 간단하기 때문에, 더 자세한 설명은 생략하도록 하겠습니다. 

 

그렇다면 실제 training에서 binary weight가 언제 활용될까요? Forward pass와 backward pass에서는 binary weight가 사용됩니다. 다만 weight를 update할 때는 full precision weight를 계산 한 뒤, 이를 위에 설명한 방식으로 binarize시켜서 forward/backward pass에 활용하는 방식입니다. Quantization으로 낮아진 accuracy를, fine tuning을 통해 full-precision accuracy 수준으로 올리게 됩니다. 

Binarization - 2) XNOR Network

XNOR network에서는 weight와 activation을 모두 binarize합니다. 단, 위에서 binary weight network에서는 양수는 1로, 음수는 -1로 맵핑했었는데요. 이번엔 한 단계를 더 거치게 됩니다. 바로 -1을 0으로 또 한 번 맵핑해주는 것입니다. 즉 양수는 1로, 음수는 0으로 맵핑한 뒤 연산을 수행하고, 계산된 값이 1이면 1로, 0이면 -1로 다시 맵핑해주는 것입니다.

 

이와 같이 binarization을 수행할 경우, 곱셈 연산을 XNOR연산으로 대체할 수 있어서 computation cost가 줄어든다는 이점이 생깁니다. XNOR 게이트가 무엇인지도 모르겠고, 0이 갑자기 왜 등장하는지도 모르겠고, 혼란스러우실텐데요. 숫자 예시를 통해 다시 천천히 설명하겠습니다. 

 

주어진 weight vector W가 (1.2, 0.8, -1.3, 0.7)이고 activation vector X가 (-1.3, -1.1, 0.7, 0.9)라고 합시다.

W를 binarize시키면 B(1, 1, -1, 1)가 되고, X를 binarize시키면 H(-1, -1, 1, 1)이 됩니다.

 

B와 H 두 벡터를 내적시킨다면 (1)*(-1) + (1)*(-1) + (-1)*(1) + (1)*(1) = (-2)가 되는데요. 방금 한 벡터 내적 연산은 multiplication + accumulation으로 구성됩니다. 

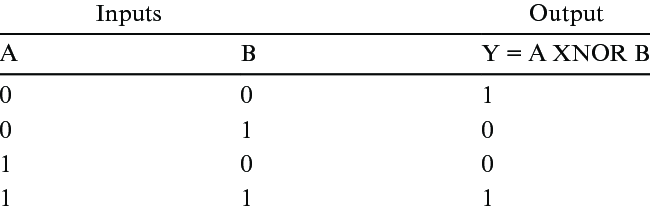
참고로 XNOR 게이트는 XOR 게이트의 negation입니다. 즉 진리표가 위와 같습니다. 그렇다면 벡터 내적 연산을 XNOR로 대체할 수 있다는 말이 무슨 뜻인지 살펴보겠습니다. 

 

만약 -1을 0으로 또 맵핑시켜준다면,  B(1, 1, -1, 1)와 H(-1, -1, 1, 1)는 각각 B' (1, 1, 0, 1)와 H' (0, 0, 1, 1)이 됩니다.

이 때, 아래의 표에서 볼 수 있듯이, (-1 / 1)의 곱셈 연산은 (0 / 1)의 XNOR연산과 똑같이 동작합니다.

예를 들어, (-1) * (1)는 (-1)이고, (0) XNOR (1)는 (0)입니다.

즉, (-1)과 (1)의 곱셈은, (0)과 (1)의 XNOR 연산 값( 0 / 1) 을 다시 (-1 / 1)로 맵핑해주는 것과 같습니다.

 

위에서 수행한 벡터 내적 연산 [ (1)*(-1) + (1)*(-1) + (-1)*(1) + (1)*(1) = (-2) ] 대신,

(1 XNOR 0), (1 XNOR 0), (0 XNOR 1), (1 XNOR 1)를 수행해서 [ 0, 0, 0, 1 ]이 나오게 되고,

이들 중 (1의 갯수)에서 (0의 갯수)를 빼주면 (1) - (3) = (-2), 같은 결과값이 구해집니다. 

결론적으로, ( multiplication +  addition)으로 수행되던 벡터 내적 연산이, (XNOR + bit count + addition)으로 대체될 수 있습니다. Multiplication은 여러 개의 게이트로 구성된 multiplier/adder를 요하는 복잡한 연산이기 때문에, 이로 인해 computation cost를 줄여주는 효과가 발생합니다. 

 

Scaling factor 알파, 베타 및 B, H를 구하는 과정은 앞서 binary weight network에서와 유사합니다. 문제는 다음과 같이 정의됩니다.

B와 H에 부호를 취하는 방식으로 B*와 H*를 구하고, 알파와 베타 또한 아까와 같이 X와 W의 l1 norm이 됩니다.

ResNet, GoogleNet에 대해 binary weight network와 xnor network 각각의 quantization을 적용한 결과는 위와 같습니다. 보다시피 결과가 영 좋지 않은데요. 무려 4년 전의 결과이기 때문에 너그러이 이해하시기 바랍니다. 이어서 2020년 모델인 ReActNet을 소개해드리겠습니다. 

Binarization - 3) ReActNet

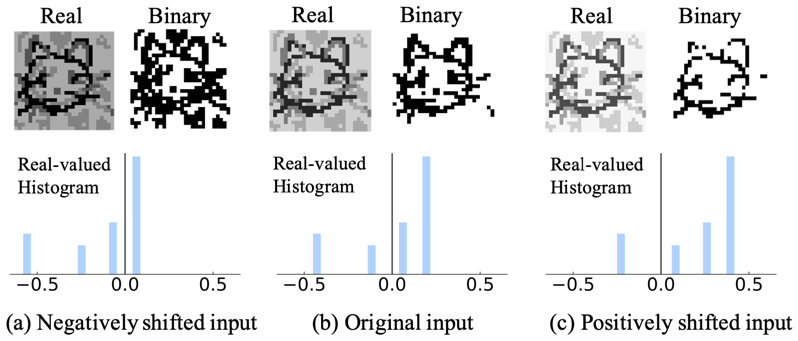
위 그림에서 하단 세 개의 히스토그램은 인풋 데이터의 분포를 나타냅니다. 상단의 이미지들은 feature map을 시각화 한 것으로, 각각 real-valued feature map과 binary valued feature map을 나타냅니다. 이를 통해 input 분포가 feature learning에 영향을 미친다는 사실을 알 수 있습니다. (a)와 같이 input 분포가 왼쪽에 쏠려 있을 경우, binary valued feature map에 노이즈가 많이 섞여 있습니다. (c)와 같이 분포가 오른쪽에 쏠려 있을 경우, binarize과정에서 정보 손실이 많이 발생했습니다. 

저자는 이러한 관찰에 기인해서, "적절한 bias"를 줘서 distribution을 변화시키자는 아이디어를 제시합니다. 즉 bias를 trainable 파라미터로 둬서 학습을 시키겠다는 것입니다. 그리하여 기존에 activation function으로 사용하던 sign 함수와 ReLU함수가 위와 같이 변형됩니다. 여기서 ReActNet 이름의 근원이 나옵니다. "Reshaping Activation"을 줄여서 ReAct라 하고, 이렇게 변형된 함수들을 RSign, RPReLU로 부릅니다. 

위 그림은 baseline 네트워크와 ReActNet 각각에 대해, normal 블락과 reduction 블락을 보여줍니다.

 

Baseline 네트워크는 MobileNetV1를 binarization을 위해 조금 수정한 버전입니다. 즉 일반적으로 사용하던 conv 대신 1-bit conv로 대체해줍니다. 1bit conv라 함은, 앞서 XNOR network에서 설명했듯이, 값을 부호에 따라 1 또는 -1로 맵핑해준 뒤, XNOR 연산으로 얻어진 1과 0들의 갯수를 세고, 그 갯수의 차를 통해 값을 얻어내는 과정을 의미합니다.

 

Baseline 네트워크는 기존 MobileNetV1의 채널 수와 레이어 수와 같은 굵직한 configuration을 그대로 사용하되, 조건에 따라 depthwise seperable convolution 블락을 normal 또는 reduction 블락으로 대체시켜줍니다. ReActNet은 거기에 추가적으로, 활성함수들을 RPReLU와 RSign으로 대체해줍니다.

 

MobileNetV1는 depthwise separable convolution, 즉 (3x3 depthwise conv + 1x1 pointwise conv)를 사용하는데요. 이러한 depthwise separable convolution 전후로 채널 수가 변하지 않을 경우 normal 블락으로 대체하고, 채널 수가 변하는 경우 reduction 블락으로 대체해줍니다. Reduction 블락의 경우, 2x2 avg pooling을 통해 채널 수를 줄였다가, activation을 복제해서 두 path로 통과시킨 뒤, 각 path의 output을 concat시키는 방식으로 채널 수를 다시 증가시켜줍니다. 

Input distribution에 따라 feature map이 크게 영향받는다는 사실을 앞서 그림을 통해 보여드렸습니다. 즉, 만약 binarize시킨 뉴럴 네트워크가, full precision 네트워크에서의 분포와 유사한 분포를 학습할 수 있다면 성능이 좋아지지 않을까 라는 생각을 할 수 있습니다. 그리하여 저자는 full precision network를 teacher 모델로, binary network를 student 모델로 두고 teacher student training을 합니다. 다만, 원래의 teature student training에서는 teacher 모델의 output logit을 사용해서 student 를 학습시키는 방식이 보편적이지만, 여기서는 목적이 분포를 유사하게 학습시키는 것이니만큼, 두 분포의 KLdivergence를 최소화시키는 방향으로 학습을 시킵니다. 

Summary

지금까지 총 세 편의 포스팅에 거쳐 quantization에 대해 설명했습니다. float32, bfloat16, int8부터 비트 수가 점점 줄이더니 급기야 binary quantization까지 살펴보았습니다. 성능이 중요한 대규모 시스템(ex. 추천 시스템)에서는 아직 16bit로 training하고, 8bit로 inference하는 것이 보편적입니다. 모바일에서는 현재 8bit가 보편적이지만, 곧 4bit가 스탠다드로 자리잡을 예정입니다. 그리고 보다시피 binary quantization도 꽤나 유망하기 때문에, 2bit가 스탠다드로 자리잡기까지도 멀지 않아 보입니다.